We introduce a training paradigm that uses plausible counterfactual explanations (p-CFEs) to match standard model accuracy while reducing reliance on spurious correlations.

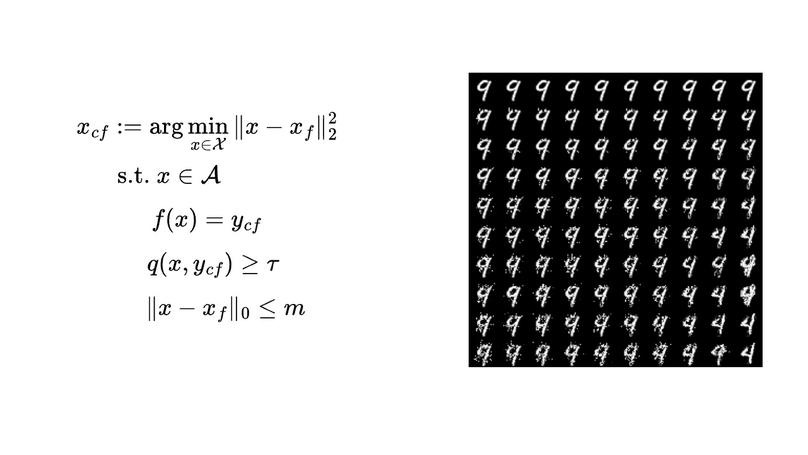
We study the problem of finding optimal sparse, manifold-aligned counterfactual explanations for classifiers. Canonically, this can be formulated as an optimization problem with multiple non-convex components, including classifier loss functions and manifold alignment (or plausibility) metrics. The added complexity of enforcing sparsity, or shorter explanations, complicates the problem further. Existing methods often focus on specific models and plausibility measures, relying on convex l_1 regularizers to enforce sparsity. In this paper, we tackle the canonical formulation using the accelerated proximal gradient (APG) method, a simple yet efficient first-order procedure capable of handling smooth non-convex objectives and non-smooth l_p (where 0 <= p < 1) regularizers. This enables our approach to seamlessly incorporate various classifiers and plausibility measures while producing sparser solutions. Our algorithm only requires differentiable data-manifold regularizers and supports box constraints for bounded feature ranges, ensuring the generated counterfactuals remain actionable. Finally, experiments on real-world datasets demonstrate that our approach effectively produces sparse, manifold-aligned counterfactual explanations while maintaining proximity to the factual data and computational efficiency.

In this paper, we present an algorithm that simultaneously generates group-wise sparse attacks within semantically meaningful areas of an image. In each iteration, the core operation of our algorithm involves the optimization of a quasinorm adversarial loss. This optimization is achieved by employing the 1/2-quasinorm proximal operator for some iterations, a method tailored for nonconvex programming. Subsequently, the algorithm transitions to a projected Nesterov’s accelerated gradient descent with 2-norm regularization applied to perturbation magnitudes. We rigorously evaluate the efficacy of our novel attack in both targeted and non-targeted attack scenarios, on CIFAR-10 and ImageNet datasets. When compared to state-of-the-art methods, our attack consistently results in a remarkable increase in group-wise sparsity, e.g., an increase of 50.9% on CIFAR-10 and 38.4% on ImageNet (average case, targeted attack), all while maintaining lower perturbation magnitudes. Notably, this performance is complemented by a significantly faster computation time and a 100% attack success rate.

Despite their impressive success in various machine learning tasks, deep neural networks are vulnerable to adversarial attacks. Through the addition of imperceptible levels of distortion to a given image, such attacks can cause a learned network to quite spectacularly misclassify the perturbed input. Several defense approaches including adversarial training and methods manipulating basis function representations of images such as JPEG compression, PCA, wavelet denoising, and soft-thresholding have shown success. The former defense works well in defending against small l_p norm attacks in the pixel representation, whereas the latter methods rely on removing high frequency signal. We show that both training-based and basis-manipulation defense methods are significantly less effective if we restrict the generation of adversarial attacks to the low frequency discrete wavelet transform (DWT) domain, thus providing new insights into vulnerabilities of deep learning models.

We present a concise optimal control optimization approach to continuous-depth deep learning models by discussing ideas and algorithms derived from the optimality conditions of the powerful Pontryagin’s Maximum Principle. The new emerging field of constant memory cost models, however, is vulnerable to adversarial attacks. Apart from highlighting the inconsistency of neural networks theoretically, we experiment with adversarial deformations for neural ordinary differential equations on MNIST and compare our results to convolutional neural-network based architectures.